T-Test
업무를 하다보면 빈번하게 개선 진행이 이루어지며, 그 결과값이 개선전과 비교하여 개선이 되었는지를 확인하는 척도로 T-Test를 진행을 해요. T-Test는 2개의 집단에 대한 비교만 가능하며, 그 이상의 집단일 경우 ANOVA를 사용해요.
일반적으로 미니탭을 많이 활용하나 요즘은 엑셀에도 통계 분석 기능이 적용이 되어 있어서 간편하게 분석해볼 수 있어요.
T-Test는 두 모집단의 평균이 같다는 귀무가설을 검정하게 되어 있어요.
(귀무가설 H0을 기각하면 개선 전에 비해 개선 후의 평균값이 달라졌다고 할 수 있으며, H0가 채택되었을 경우에는 개선 전과 후의 평균 차이는 없다고 볼 수 있다.)
H0: μ1 - μ2 = 0 - 귀무가설
H1: μ1 - μ2 ≠ 0 - 대립가설
1) 예제
아래와 같이 여학생 6명과 남학생 5명의 학습 시간을 확인할 수 있다.

여학생과 남학생의 학습 시간은 같다고 할 수있을까?
귀무가설과 대립가설은 하기와 같다.
H0 = 여학생과 남학생의 학습 시간은 같다.
H1 = 여학생과 남학생의 학습 시간은 다르다.
2) 엑셀 따라하기
1. 데이터탭 -> 데이터 분석 -> t-검정: 이분산 가정 두집단
(등분산 : 두 집단의 분산이 같을 경우 / 이분산 : 두 집단의 분산이 다를 경우)

2. 변수1 = 여학생의 값 범위 / 변수2 = 남학생의 값 범위를 입력 후 확인

3. 값 해석하기

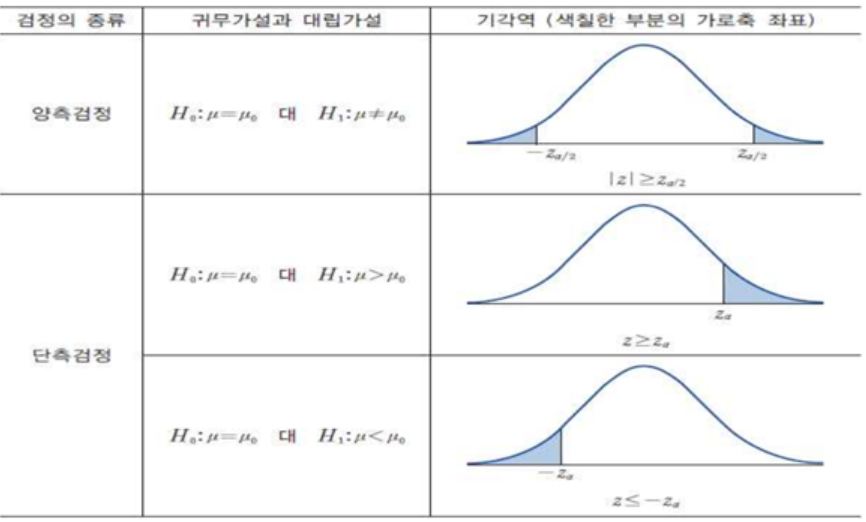
우선 예제에서 궁금했던 여학생과 남학생의 학습 시간에 대한 판단 기준은 양의값과 음의값의 기준이 있으므로 양측 검증으로 판단하게 됩니다.
결과값에서 t 기각치 양측검증의 값이 2.364이므로, -2.364 < 1.472 < 2.364가 되며 이는 기각치 내에 존재하므로 귀무가설을 기각하지 않게 됩니다.
또한 P-Value의 양측 검정 값은 0.184로 유의수준 0.05보다 크므로 귀무가설을 기각하지 않습니다.
결과로 여학생과 남학생 간의 학습 시간은 크게 다르다고 말할만큼 설득력이 없다고 할 수 있습니다.
'STUDY > 통계' 카테고리의 다른 글
| 3그룹(또는 그 이상)의 평균값이 차이가 있을까? - 엑셀로 분산분석(ANOVA)하는 방법 (0) | 2020.11.25 |
|---|---|
| 변수끼리 얼마나 연관성이 있을까? - 엑셀로 상관관계분석하기 (0) | 2020.11.17 |
| 런차트(Run chart)의 이해_ Minitab 미니탭 (0) | 2020.03.29 |
| 확률과 분포 (0) | 2019.11.25 |
| 2요인실험 - ANOVA (0) | 2019.11.21 |
| P-Value_유의확률의 이해 (0) | 2019.11.13 |